Questions: Look at this diagram: If P R and S U are parallel lines and m angle P Q O=132°, what is m angle R Q O?

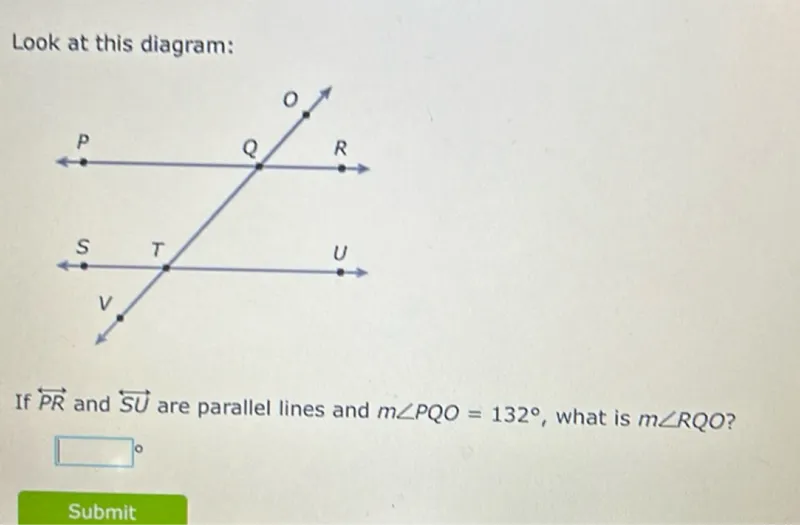
Transcript text: Look at this diagram: If $\overleftrightarrow{P R}$ and $\overleftrightarrow{S U}$ are parallel lines and $m \angle P Q O=132^{\circ}$, what is $m \angle R Q O$ ?

Solution

Solution Steps

Step 1: Analyze the given information

We are given that lines PR and SU are parallel. We are also given that the angle PQO measures 132 degrees. We want to find the measure of angle RQO.

Step 2: Identify the relationship between angles PQO and RQO

Angles PQO and RQO are adjacent angles that form a straight line. Therefore, they are supplementary angles. This means their measures add up to 180 degrees.

Step 3: Set up the equation and solve for m∠RQO

Since angles PQO and RQO are supplementary, we can write the equation:

$m\angle PQO + m\angle RQO = 180^\circ$

Substitute the given value of $m\angle PQO = 132^\circ$ into the equation:

$132^\circ + m\angle RQO = 180^\circ$

Subtract 132 from both sides:

$m\angle RQO = 180^\circ - 132^\circ$

$m\angle RQO = 48^\circ$