Questions: y=1/2 x-1 y=1/2 x+5 How many solutions does the system of equations have? no solution one solution infinitely many solutions
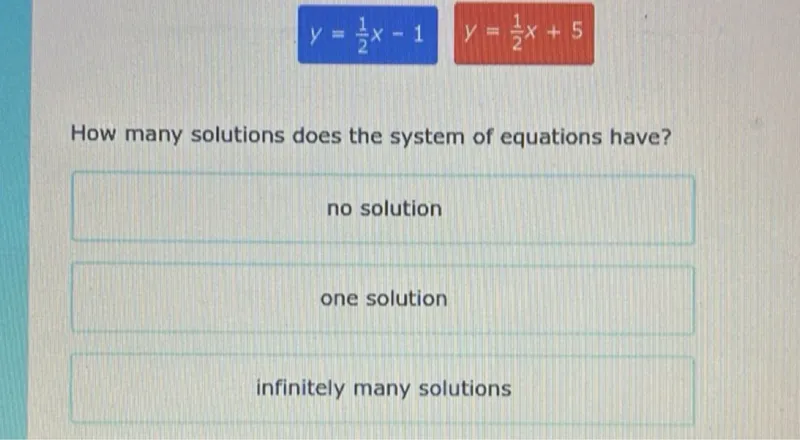
Transcript text: \[
y=\frac{1}{2} x-1 \quad y=\frac{1}{2} x+5
\]
How many solutions does the system of equations have?
no solution
one solution
infinitely many solutions





