Questions: Solve the equation. m/4 + 5 = m/3 + 7 m = (Type an integer or fraction. Simplify your answer.)

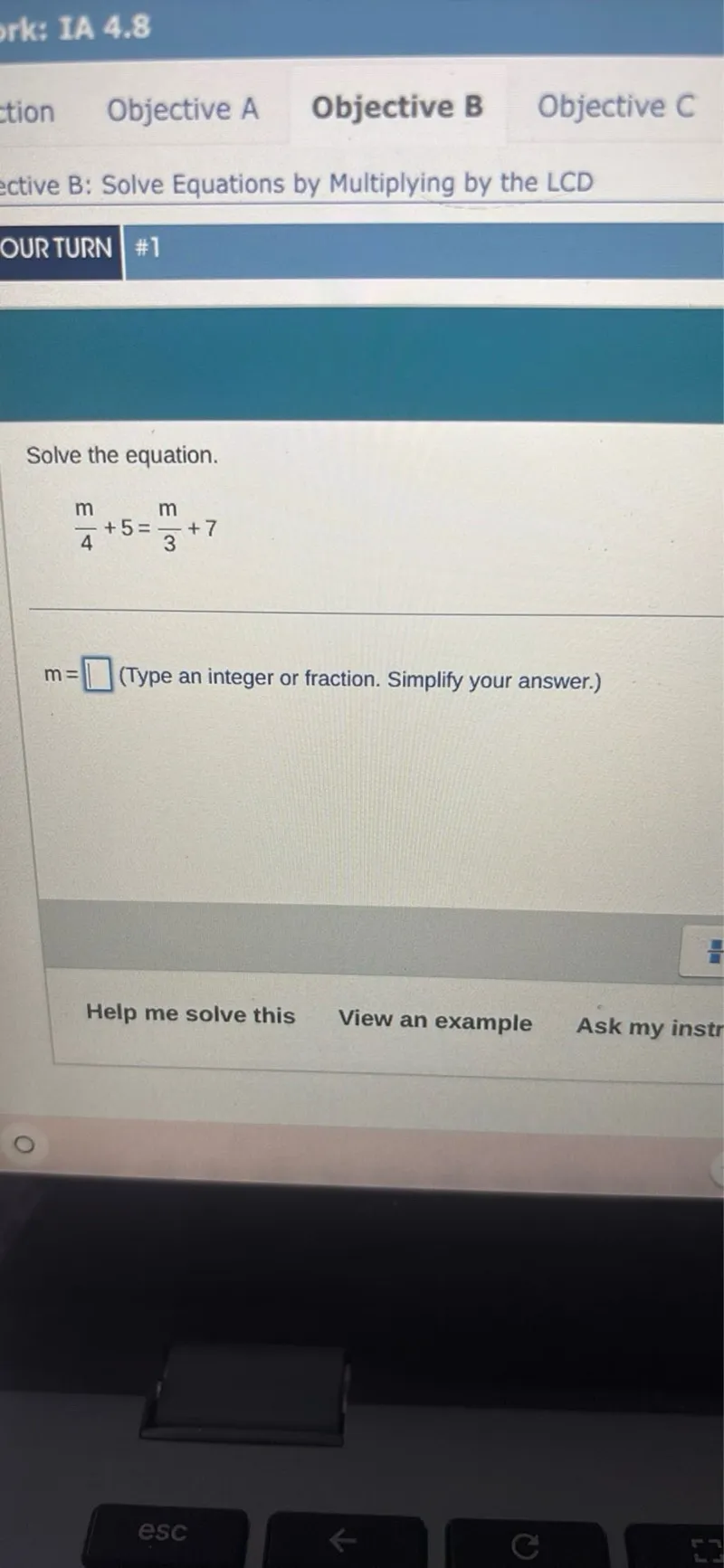
$Solve the equation. m/4 + 5 = m/3 + 7 m = (Type an integer or fraction. Simplify your answer.)$

Transcript text: Solve the equation. \[ \frac{m}{4}+5=\frac{m}{3}+7 \] $\mathrm{m}=$ $\square$ (Type an integer or fraction. Simplify your answer.)

Solution

Solution Steps

Step 1: Eliminate the fractions by multiplying both sides by the LCD

The least common denominator (LCD) of the fractions $\frac{m}{4}$ and $\frac{m}{3}$ is 12. Multiply both sides of the equation by 12 to eliminate the denominators: \[ 12 \left( \frac{m}{4} + 5 \right) = 12 \left( \frac{m}{3} + 7 \right). \]

Step 2: Distribute and simplify

Distribute 12 to each term inside the parentheses: \[ 12 \cdot \frac{m}{4} + 12 \cdot 5 = 12 \cdot \frac{m}{3} + 12 \cdot 7. \] Simplify each term: \[ 3m + 60 = 4m + 84. \]

Step 3: Solve for $m$

Subtract $3m$ from both sides to isolate the variable: \[ 60 = m + 84. \] Subtract 84 from both sides: \[ 60 - 84 = m. \] Simplify: \[ m = -24. \]