Questions: A small hole in the wing of a space shuttle requires a 16.3 cm^2 patch. What is the patch's area in square kilometers (km^2) ? Be sure your answer has the correct number of significant figures. 1.63 x 10^-9 km^2 If the patching material costs NASA 2.85 / in^2, what is the cost of the patch to the nearest cent? Be sure your answer has the correct number of significant figures.

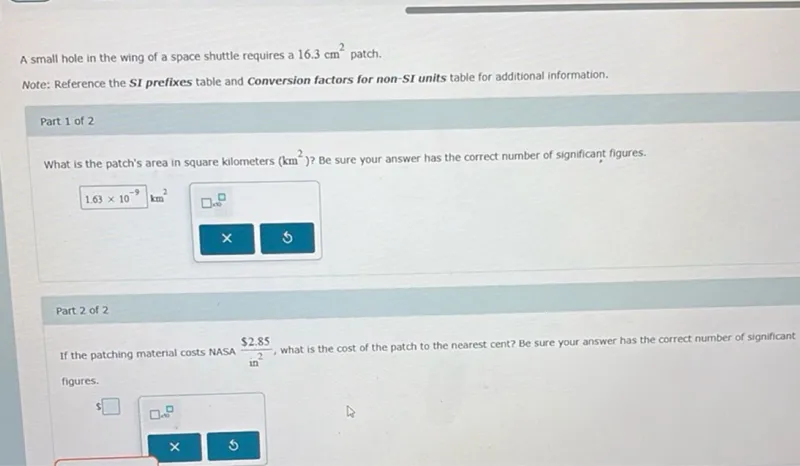
A small hole in the wing of a space shuttle requires a 16.3 cm^2 patch. What is the patch's area in square kilometers (km^2) ? Be sure your answer has the correct number of significant figures. 1.63 x 10^-9 km^2 If the patching material costs NASA 2.85 / in^2, what is the cost of the patch to the nearest cent? Be sure your answer has the correct number of significant figures.
Transcript text: A small hole in the wing of a space shuttle requires a $16.3 \mathrm{~cm}^{2}$ patch. What is the patch's area in square kilometers $\left(\mathrm{km}^{2}\right)$ ? Be sure your answer has the correct number of significant figures. \[ 1.63 \times 10^{-9} \mathrm{~km}^{2} \] If the patching material costs NASA $\frac{\$ 2.85}{\text { in }^{2}}$, what is the cost of the patch to the nearest cent? Be sure your answer has the correct number of significant figures.
failed

Solution

failed
failed

Solution Steps

Step 1: Convert \(\mathrm{cm}^2\) to \(\mathrm{km}^2\)
  1. The area of the patch is \(16.3 \, \mathrm{cm}^2\).
  2. Convert \(\mathrm{cm}^2\) to \(\mathrm{m}^2\): \(1 \, \mathrm{cm}^2 = 10^{-4} \, \mathrm{m}^2\).
  3. Therefore, \(16.3 \, \mathrm{cm}^2 = 16.3 \times 10^{-4} \, \mathrm{m}^2 = 0.00163 \, \mathrm{m}^2\).
  4. Convert \(\mathrm{m}^2\) to \(\mathrm{km}^2\): \(1 \, \mathrm{m}^2 = 10^{-6} \, \mathrm{km}^2\).
  5. Therefore, \(0.00163 \, \mathrm{m}^2 = 0.00163 \times 10^{-6} \, \mathrm{km}^2 = 1.63 \times 10^{-9} \, \mathrm{km}^2\).
Step 2: Convert \(\mathrm{cm}^2\) to \(\mathrm{in}^2\)
  1. The area of the patch is \(16.3 \, \mathrm{cm}^2\).
  2. Convert \(\mathrm{cm}^2\) to \(\mathrm{in}^2\): \(1 \, \mathrm{cm}^2 = 0.155 \, \mathrm{in}^2\).
  3. Therefore, \(16.3 \, \mathrm{cm}^2 = 16.3 \times 0.155 \, \mathrm{in}^2 = 2.5265 \, \mathrm{in}^2\).
Step 3: Calculate the cost of the patch
  1. The cost of the patching material is \(\$2.85\) per \(\mathrm{in}^2\).
  2. The area of the patch is \(2.5265 \, \mathrm{in}^2\).
  3. Therefore, the cost of the patch is \(2.5265 \, \mathrm{in}^2 \times \$2.85/\mathrm{in}^2 = \$7.198525\).
  4. Round to the nearest cent: \(\$7.20\).

Final Answer

Part 1: \( \boxed{1.63 \times 10^{-9} \, \mathrm{km}^2} \)

Part 2: \$ \( \boxed{7.20} \)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Factor the binomial completely. s^3 - 729 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. s^3 - 729 = (Factor completely.) B. The binomial is prime.
failedAnswered
The energy of an object is given by E=mg h + 1/2 m(dh/dt)^2 where m is the (constant) mass of the object, g is constant, and h is the height of the object. If the energy of the object is increasing at a rate of 50 ft. lbs. / sec, find the acceleration of the object the instant its velocity is 10 ft / sec.
failedAnswered
Refer to the results of the accompanying study. Complete parts (a) through (e) below. B. The mean is very close to the sample mean, 306/659, not the mean found in part (b). The standard deviation though is very close the theoretical standard deviation from part (b). C. These values are very close to the theoretical values from part (b). D. The mean is very close to the theoretical mean from part (b), but the standard deviation does not seem to follow the theoretical standard deviation from part (b). (d) Describe the shape of the distributions of outcomes from the simulation in part (c). Compute n p(1-p) where p=0.5 (the proportion stated in the null hypothesis). Based on this result is the distribution of p̂ approximately normal? Since n p(1-p)= 164.75 10 and the sample size is less than 5% of the population size (assuming the TV personality has made at least the necessary number of predictions, which is a reasonable assumption), the distribution of the sample proportion, p̂, is approximately normal. (e) Use the normal model to find P(p̂ ≤ 0.464), where 0.464=306/659, the sample proportion of correct predictions made by the TV personality. P(p̂ ≤ 0.464)=
failedAnswered
A 3125 ft^3 open-top rectangular tank with a square base x ft on a side and y ft deep is to be built with its top flush with the ground to catch runoff water. The costs associated with the tank involve not only the material from which the tank is made but also an excavation charge proportional to the product xy. a. If the total cost is c=6(x^2+4xy)+36xy, what values of x and y will minimize it? b. Give a possible scenario for the cost function in part (a). a. The values of x and y that minimize the cost are x= and y= The minimum cost is .
failedAnswered
The wheels are in motion It's certainly not downhill from here. Yogi talked of a utensil In this case it's unusually clear. A funny name for a convention site And for hunters to take a break There may be something that blocks your way Why's it there for heaven's sake?