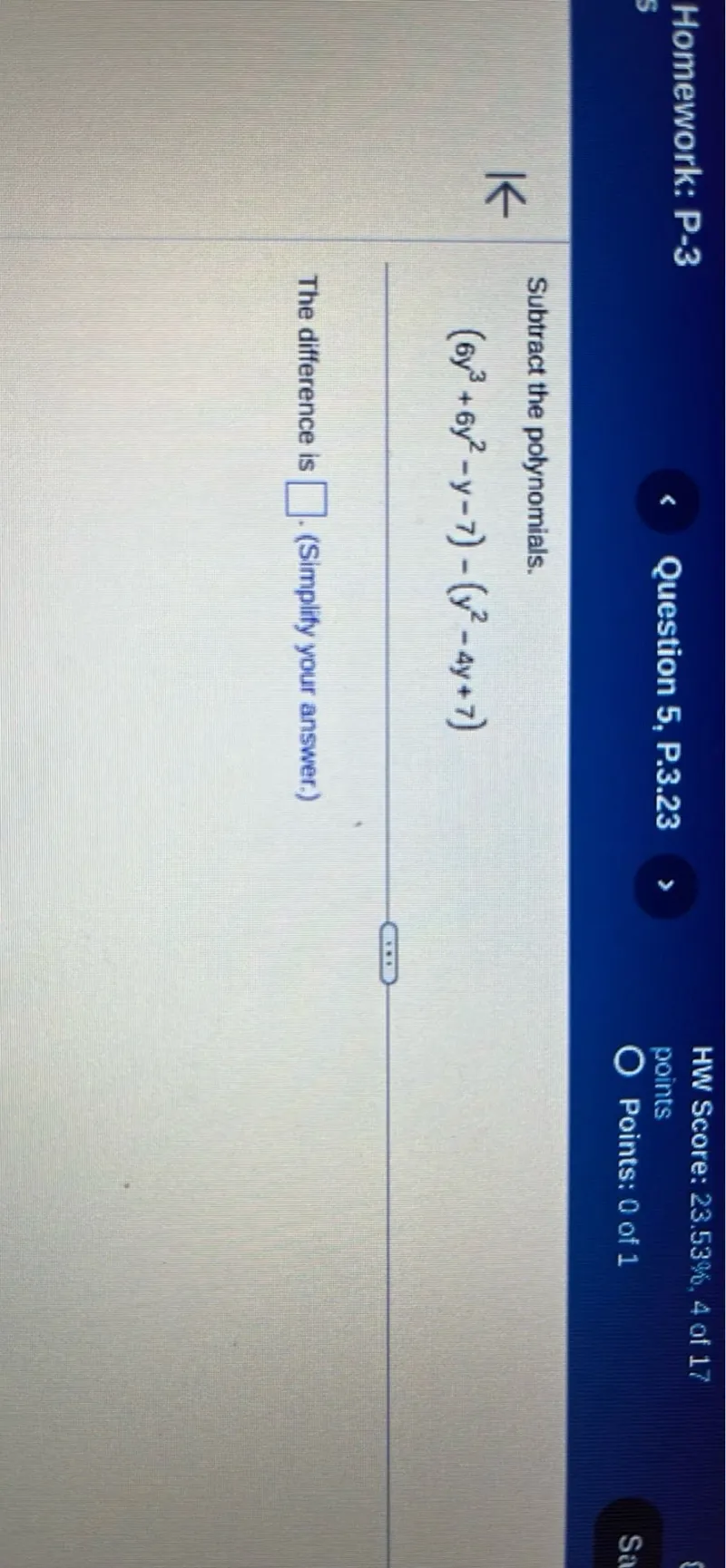
Questions: Homework: P-3 Question 5, P.3.23 HW Score: 23.53%, 4 of 17 points Points: 0 of 1 Subtract the polynomials. (6y^3+6y^2-y-7)-(y^2-4y+7) The difference is . (Simplify your answer.)

Solution Steps

Subtract the second polynomial by distributing the negative sign to each term inside the parentheses: \[ \left(6 y^{3}+6 y^{2}-y-7\right) - y^{2} + 4y - 7 \]

Combine the terms with the same degree of \( y \):

• \( 6y^3 \) remains as is.
• \( 6y^2 - y^2 = 5y^2 \).
• \( -y + 4y = 3y \).
• \( -7 - 7 = -14 \).

Combine the results from Step 2 to write the simplified polynomial: \[ 6y^3 + 5y^2 + 3y - 14 \]

The difference is \(\boxed{6y^3 + 5y^2 + 3y - 14}\).

Final Answer