Questions: Perform the following operation and express in simplest form. 4x / (x^2 + x - 42) ÷ x^3 / (x^2 - 49)
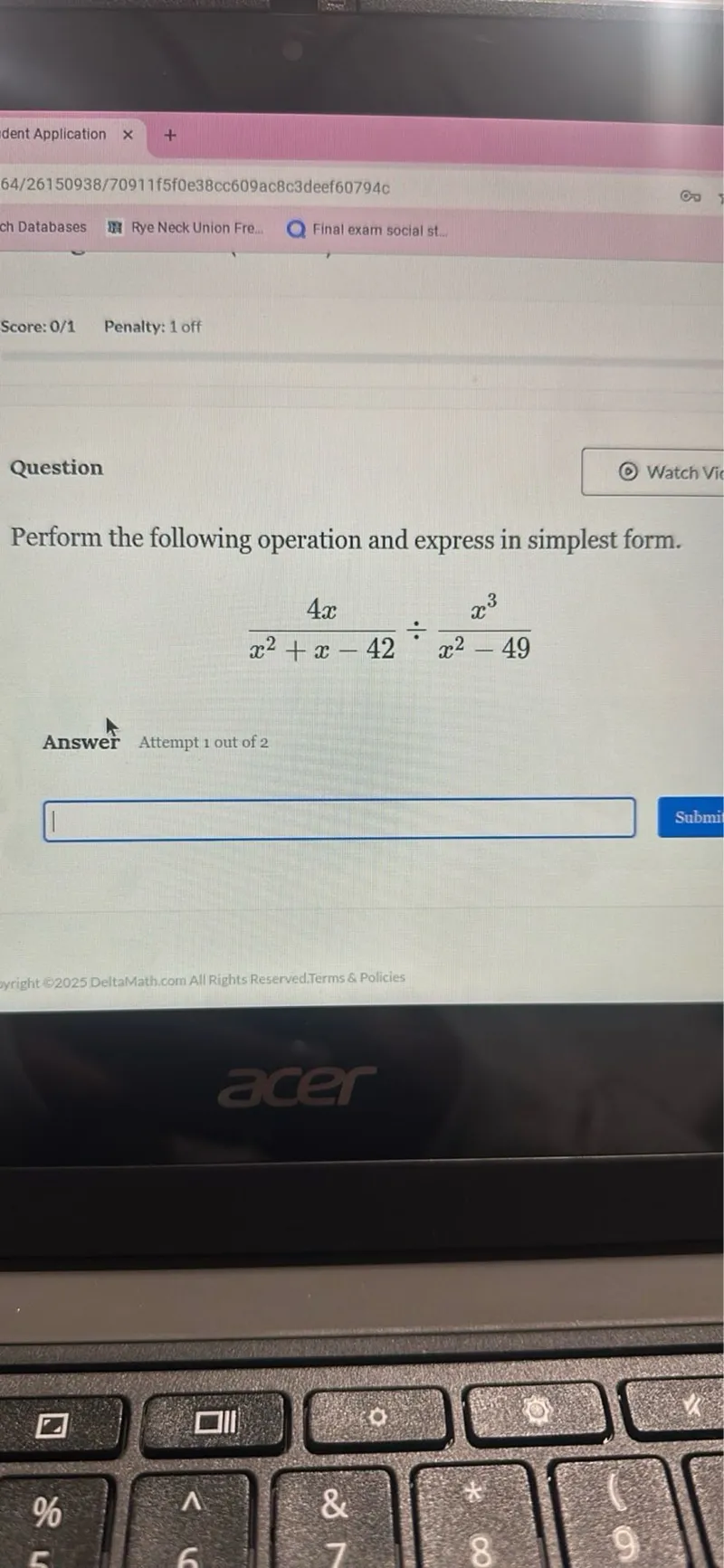
Transcript text: Perform the following operation and express in simplest form.
\[
\frac{4 x}{x^{2}+x-42} \div \frac{x^{3}}{x^{2}-49}
\]





