Questions: Sets L and H are defined as follows. L=-2,4,8 H=-2,1,7 Answer each part below. Write your answer in roster form or as ∅. (a) Find the intersection of L and H. L ∩ H= (b) Find the union of L and H. L ∪ H=

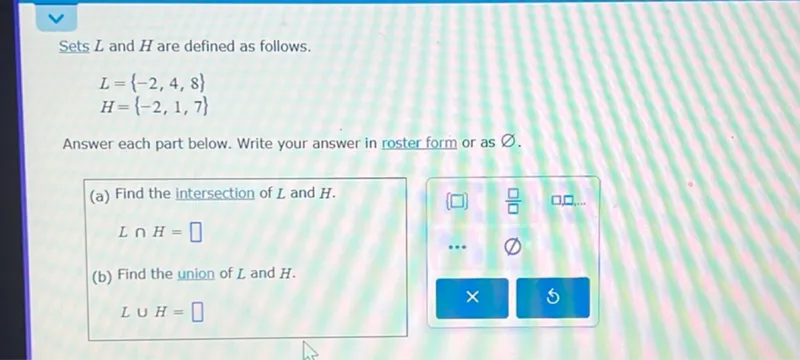
Sets L and H are defined as follows.
L=-2,4,8
H=-2,1,7

Answer each part below. Write your answer in roster form or as ∅.
(a) Find the intersection of L and H.
L ∩ H=

(b) Find the union of L and H.
L ∪ H=

Transcript text: Sets $L$ and $H$ are defined as follows. \[ \begin{array}{l} L=\{-2,4,8\} \\ H=\{-2,1,7\} \end{array} \] Answer each part below. Write your answer in roster form or as $\varnothing$. (a) Find the intersection of $L$ and $H$. \[ L \cap H= \] $\square$ (b) Find the union of $L$ and $H$. \[ L \cup H= \] $\square$

Solution

Solution Steps

Step 1: Identify the elements of sets \( L \) and \( H \)

Set \( L = \{-2, 4, 8\} \)
Set \( H = \{-2, 1, 7\} \)

Step 2: Find the intersection of \( L \) and \( H \)

The intersection \( L \cap H \) consists of elements that are common to both sets.
The common element is \(-2\).
Therefore, \( L \cap H = \{-2\} \).

Step 3: Find the union of \( L \) and \( H \)

The union \( L \cup H \) consists of all unique elements from both sets.
Combining the elements of \( L \) and \( H \), we get \(\{-2, 1, 4, 7, 8\}\).
Therefore, \( L \cup H = \{-2, 1, 4, 7, 8\} \).

Final Answer

(a) \( L \cap H = \boxed{\{-2\}} \)

(b) \( L \cup H = \boxed{\{-2, 1, 4, 7, 8\}} \)

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!