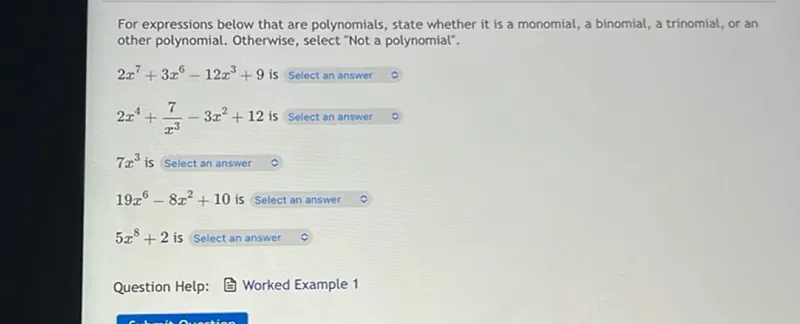
Questions: 2x^7+3x^6-12x^3+9 is Select an answer 2x^4+7/x^3-3x^2+12 is Select an answer 7x^3 is Select an answer 19x^6-8x^2+10 is Select an answer 5x^8+2 is Select an answer

2x^7+3x^6-12x^3+9 is Select an answer 2x^4+7/x^3-3x^2+12 is Select an answer 7x^3 is Select an answer 19x^6-8x^2+10 is Select an answer 5x^8+2 is Select an answer
Transcript text: $2 x^{7}+3 x^{6}-12 x^{3}+9$ is Select an answer $2 x^{4}+\frac{7}{x^{3}}-3 x^{2}+12$ is Select an answer $7 x^{3}$ is Select an answer $19 x^{6}-8 x^{2}+10$ is Select an answer $5 x^{8}+2$ is Select an answer
failed

Solution

failed
failed

Determine whether \(2x^{7} + 3x^{6} - 12x^{3} + 9\) is a monomial, binomial, trinomial, other polynomial, or not a polynomial.

Step subtitle: Identify the number of terms

The expression \(2x^{7} + 3x^{6} - 12x^{3} + 9\) has four terms: \(2x^{7}\), \(3x^{6}\), \(-12x^{3}\), and \(9\).

Step subtitle: Classify the polynomial

Since the expression has four terms, it is classified as an "other polynomial."

\(\boxed{\text{Other polynomial}}\)

Determine whether \(2x^{4} + \frac{7}{x^{3}} - 3x^{2} + 12\) is a monomial, binomial, trinomial, other polynomial, or not a polynomial.

Step subtitle: Check for polynomial conditions

The term \(\frac{7}{x^{3}}\) can be rewritten as \(7x^{-3}\), which has a negative exponent. Polynomials cannot have negative exponents.

Step subtitle: Conclusion

Since the expression contains a term with a negative exponent, it is not a polynomial.

\(\boxed{\text{Not a polynomial}}\)

Determine whether \(7x^{3}\) is a monomial, binomial, trinomial, other polynomial, or not a polynomial.

Step subtitle: Identify the number of terms

The expression \(7x^{3}\) has only one term.

Step subtitle: Classify the polynomial

Since the expression has one term, it is classified as a "monomial."

\(\boxed{\text{Monomial}}\)

Determine whether \(19x^{6} - 8x^{2} + 10\) is a monomial, binomial, trinomial, other polynomial, or not a polynomial.

Step subtitle: Identify the number of terms

The expression \(19x^{6} - 8x^{2} + 10\) has three terms: \(19x^{6}\), \(-8x^{2}\), and \(10\).

Step subtitle: Classify the polynomial

Since the expression has three terms, it is classified as a "trinomial."

\(\boxed{\text{Trinomial}}\)

Determine whether \(5x^{8} + 2\) is a monomial, binomial, trinomial, other polynomial, or not a polynomial.

Step subtitle: Identify the number of terms

The expression \(5x^{8} + 2\) has two terms: \(5x^{8}\) and \(2\).

Step subtitle: Classify the polynomial

Since the expression has two terms, it is classified as a "binomial."

\(\boxed{\text{Binomial}}\)

\(\boxed{\text{Other polynomial}}\)
\(\boxed{\text{Not a polynomial}}\)
\(\boxed{\text{Monomial}}\)
\(\boxed{\text{Trinomial}}\)
\(\boxed{\text{Binomial}}\)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
The equilibrium constant for the reaction: PCl5 ⇌ PCl3 + Cl2 is 0.0245 at 25°C. What molar concentration of PCl5 would be present at equilibrium if the concentrations of PCl3 and Cl2 were both 0.227 M?
failedAnswered
1.1.8 Quiz: Analyze Organizing Paragraphs Question / ot 10 Read this passage: Funland owner Wyatt Martinez is very proud of the amusement park he helped his father build. As a child Martinez watched his father run Funland and dreamed of turning it into the 110 -acre park it is today. After business school, Martinez began to plan for Funland's expansion. Less than six years later, Funland was named one of the top five amusement parks in the country. Martinez hopes to one day pass ownership of Funland down to his children. His greatest wish is to see Funland continue to grow and be a destination for families from all over the country. What is the main idea of this paragraph? A. The growth of Funland's size and popularity B. The history of how Martinez's father began Funland C. Wyatt Martinez and his relationship with Funland D. Martinez's future plans for expanding Funland
failedAnswered
Suppose a researcher wants to investigate the effect of the amount of fertilizer on the height of a common houseplant. More specifically, the researcher is interested in determining if there is a difference between the mean heights of the plants receiving one of three different fertilizer levels: high, medium, and low. Which of the following would be the correct null hypothesis? H0: μ1=μ2 H0: μ1=μ2=μ3 H0: μ1=μ2=μ3=μ4 HA: μ1=μ2=μ3
failedAnswered
Identifying the intermolecular forces between atoms, ions and molecules. What kind of intermolecular forces act between a carbon monoxide molecule and a hydrogen chloride molecule?
failedAnswered
Determine whether the following statements are true and give an explanation or counterexample. a. All polynomials are rational functions but not all rational functions are polynomials. b. If f is a linear polynomial, then f o f is a quadratic polynomial. c. If f and g are polynomials, then the degrees of f ∘ g and g ∘ f are equal. d. To graph g(x)=f(x+2), shift the graph of f two units to the right. b. Choose the correct answer below. A. The statement is true. Let f(x)=ax+b be a linear function where a and b are constants. Then f ∘ f=(ax+b)(ax+b)=a^2 x^2+2abx+b^2. B. The statement is true. The degree of the composition function f ∘ g is the sum or the degrees of the functions f and g. If both functions are linear, the sum of their degrees is 2. C. The statement is false. Let f(x)=x+2. Then f ∘ f=f(f(x))=(x+2)+2=x+4. This is a linear function.