Questions: Each of the following sequences is either arithmetic or geometric. Identify the sequence: a. 1,10,19,28, ... b. 90,130,170, ... c. 3,6,12, ... d. 15, 15^5, 15^9, 15^13, ... a. Is the sequence arithmetic or geometric? - Arithmetic - Geometric The next three terms of 1,10,19,28, ... are 37,46, and 55. (Simplify your answers. Type whole numbers. Use ascending order.) b. Is the sequence arithmetic or geometric? - Arithmetic - Geometric

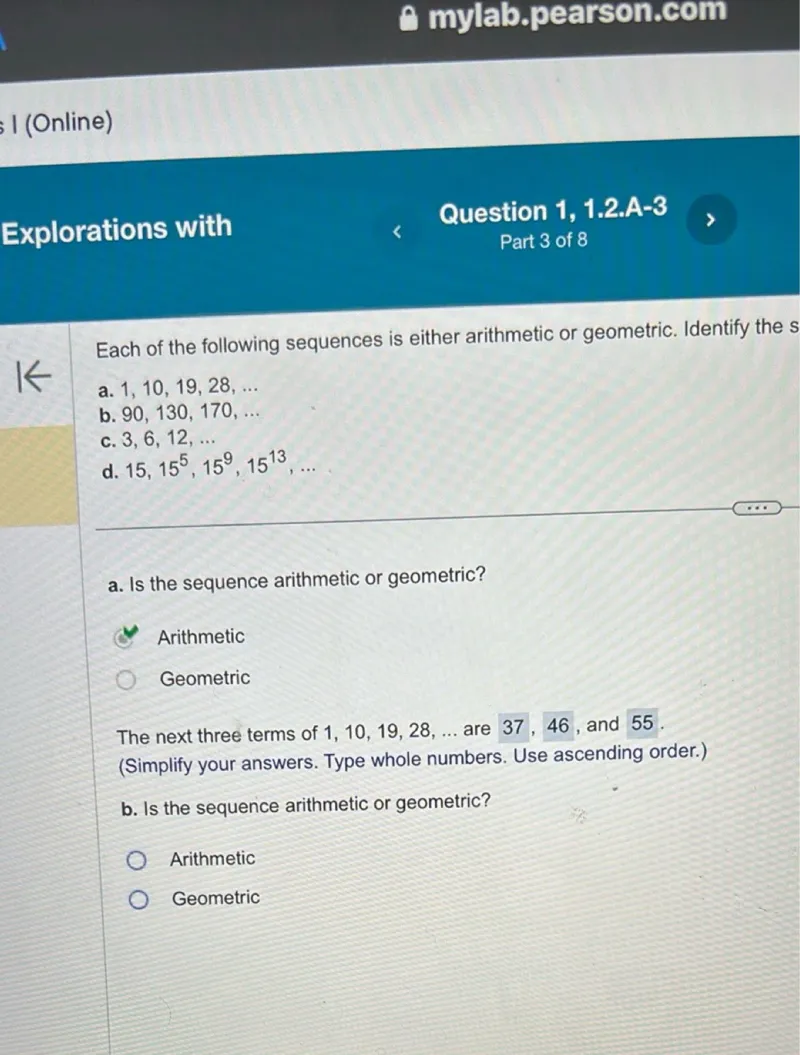
Identify whether the sequence \(1, 10, 19, 28, \ldots\) is arithmetic or geometric.

Check for arithmetic sequence

An arithmetic sequence has a common difference between consecutive terms. Calculate the differences:
\(10 - 1 = 9\),
\(19 - 10 = 9\),
\(28 - 19 = 9\).
The common difference is \(9\), so the sequence is arithmetic.

Check for geometric sequence

A geometric sequence has a common ratio between consecutive terms. Calculate the ratios:
\(\frac{10}{1} = 10\),
\(\frac{19}{10} = 1.9\),
\(\frac{28}{19} \approx 1.47\).
The ratios are not equal, so the sequence is not geometric.

The sequence is \(\boxed{\text{Arithmetic}}\).

Find the next three terms of the sequence \(1, 10, 19, 28, \ldots\).

Calculate the next terms

The common difference is \(9\). Add \(9\) to the last term repeatedly:
\(28 + 9 = 37\),
\(37 + 9 = 46\),
\(46 + 9 = 55\).

The next three terms are \(\boxed{37, 46, 55}\).

Identify whether the sequence \(90, 130, 170, \ldots\) is arithmetic or geometric.

Check for arithmetic sequence

Calculate the differences:
\(130 - 90 = 40\),
\(170 - 130 = 40\).
The common difference is \(40\), so the sequence is arithmetic.

Check for geometric sequence

Calculate the ratios:
\(\frac{130}{90} \approx 1.44\),
\(\frac{170}{130} \approx 1.31\).
The ratios are not equal, so the sequence is not geometric.

The sequence is \(\boxed{\text{Arithmetic}}\).

Identify whether the sequence \(3, 6, 12, \ldots\) is arithmetic or geometric.

Check for arithmetic sequence

Calculate the differences:
\(6 - 3 = 3\),
\(12 - 6 = 6\).
The differences are not equal, so the sequence is not arithmetic.

Check for geometric sequence

Calculate the ratios:
\(\frac{6}{3} = 2\),
\(\frac{12}{6} = 2\).
The common ratio is \(2\), so the sequence is geometric.

The sequence is \(\boxed{\text{Geometric}}\).

Identify whether the sequence \(15, 15^{5}, 15^{9}, 15^{13}, \ldots\) is arithmetic or geometric.

Check for arithmetic sequence

Calculate the differences:
\(15^{5} - 15 = 759375 - 15 = 759360\),
\(15^{9} - 15^{5} = 38443359375 - 759375 = 38442600000\).
The differences are not equal, so the sequence is not arithmetic.

Check for geometric sequence

Calculate the ratios:
\(\frac{15^{5}}{15} = 15^{4} = 50625\),
\(\frac{15^{9}}{15^{5}} = 15^{4} = 50625\).
The common ratio is \(50625\), so the sequence is geometric.

The sequence is \(\boxed{\text{Geometric}}\).

The sequence \(1, 10, 19, 28, \ldots\) is \(\boxed{\text{Arithmetic}}\), and the next three terms are \(\boxed{37, 46, 55}\).
The sequence \(90, 130, 170, \ldots\) is \(\boxed{\text{Arithmetic}}\).
The sequence \(3, 6, 12, \ldots\) is \(\boxed{\text{Geometric}}\).
The sequence \(15, 15^{5}, 15^{9}, 15^{13}, \ldots\) is \(\boxed{\text{Geometric}}\).