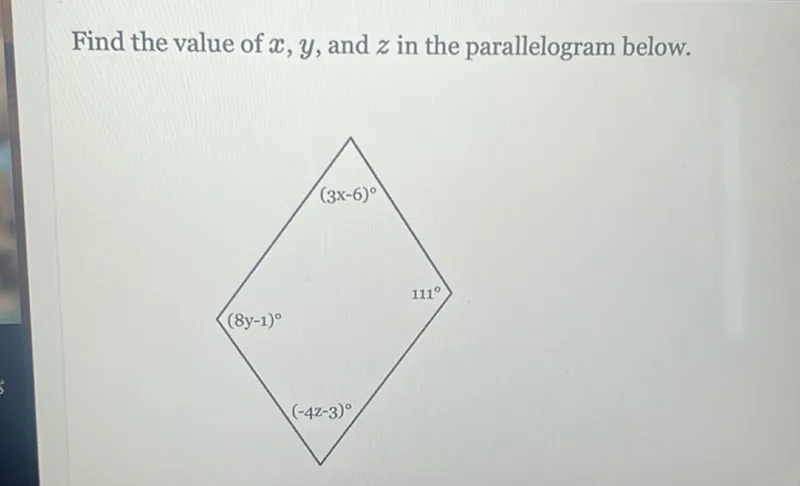
Find the value of $x$.
Set up an equation.
In a parallelogram, consecutive angles are supplementary, so their sum is 180°. Therefore, we have the equation:
\( (3x - 6) + 111 = 180 \)
Simplify the equation.
\( 3x + 105 = 180 \)
Subtract 105 from both sides.
\( 3x = 180 - 105 \)
\( 3x = 75 \)
Divide both sides by 3.
\( x = \frac{75}{3} \)
\( x = 25 \)
\( \boxed{x = 25} \)
Find the value of $y$.
Set up an equation.
In a parallelogram, opposite angles are equal. Therefore, we have the equation:
\( 8y - 1 = 111 \)
Add 1 to both sides.
\( 8y = 111 + 1 \)
\( 8y = 112 \)
Divide both sides by 8.
\( y = \frac{112}{8} \)
\( y = 14 \)
\( \boxed{y = 14} \)
Find the value of $z$.
Set up an equation.
In a parallelogram, consecutive angles are supplementary, so their sum is 180°. Therefore, we have the equation:
\( 111 + (-4z - 3) = 180 \)
Simplify the equation.
\( 111 - 4z - 3 = 180 \)
\( 108 - 4z = 180 \)
Subtract 108 from both sides.
\( -4z = 180 - 108 \)
\( -4z = 72 \)
Divide both sides by -4.
\( z = \frac{72}{-4} \)
\( z = -18 \)
\( \boxed{z = -18} \)
\( \boxed{x = 25} \)
\( \boxed{y = 14} \)
\( \boxed{z = -18} \)