Questions: Truck Pollution: In an experiment to determine the effect of ambient temperature on the emissions of oxides of nitrogen (NOX) of diesel trucks, ten trucks were run at temperatures of 40 degrees F and 80 degrees F. The emissions, in parts per billion, are presented in the following table. Truck 40 degrees F 80 degrees F 1 838.7 817.8 2 752.8 764.9 3 856.9 843.0 4 901.0 796.1 5 784.1 763.2 6 863.2 821.3 7 881.3 783.4 8 739.4 695.5 9 749.5 771.6 10 848.6 795.7
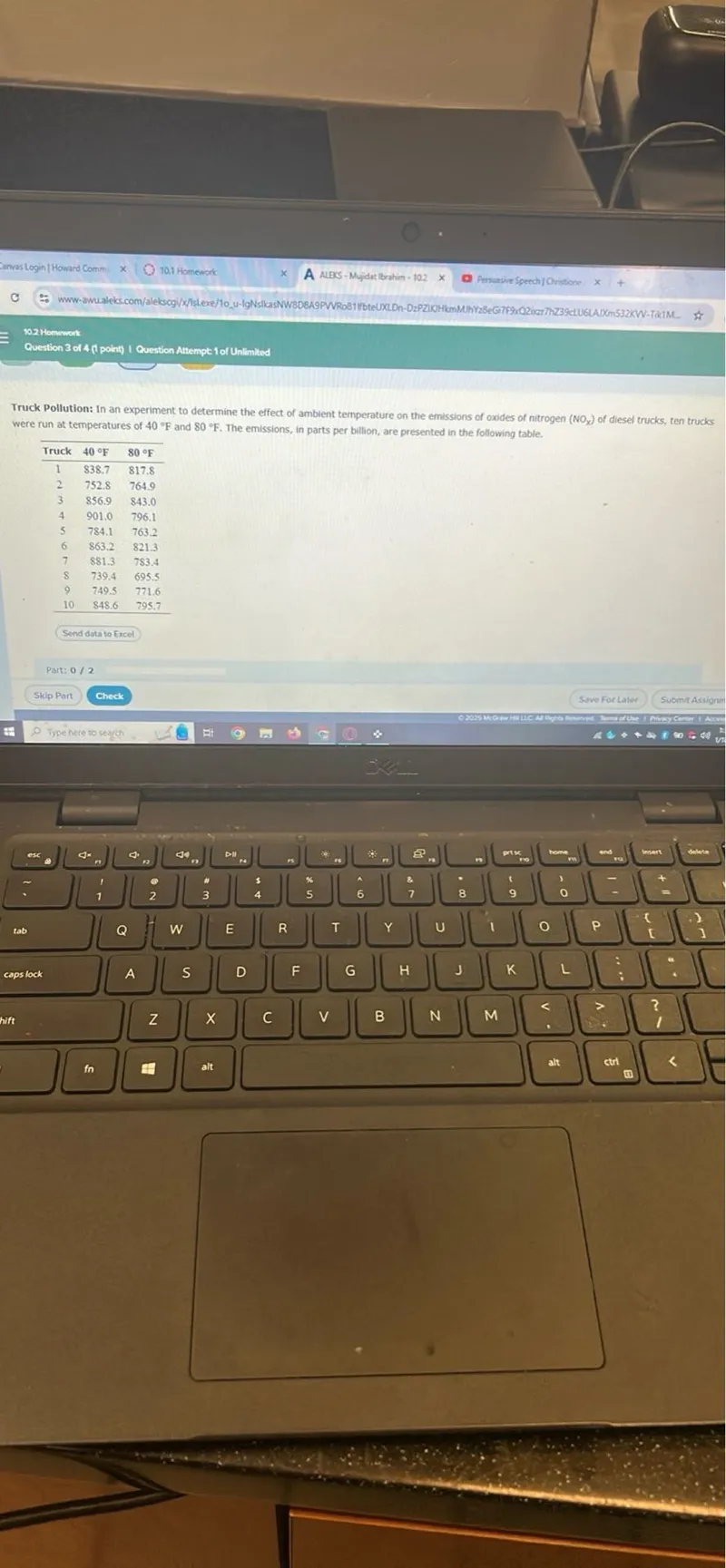
Transcript text: Truck Pollution: In an experiment to determine the effect of ambient temperature on the emissions of oxides of nitrogen (NOX) of diesel trucks, ten trucks were run at temperatures of $40^{\circ} \mathrm{F}$ and $80^{\circ} \mathrm{F}$. The emissions, in parts per billion, are presented in the following table.
\begin{tabular}{ccc}
\hline Truck & $40^{\circ} \mathrm{F}$ & $80^{\circ} \mathrm{F}$ \\
\hline 1 & 838.7 & 817.8 \\
2 & 752.8 & 764.9 \\
3 & 856.9 & 843.0 \\
4 & 901.0 & 796.1 \\
5 & 784.1 & 763.2 \\
6 & 863.2 & 821.3 \\
7 & 881.3 & 783.4 \\
8 & 739.4 & 695.5 \\
9 & 749.5 & 771.6 \\
10 & 848.6 & 795.7 \\
\hline
\end{tabular}





