Questions: Complete the following table by stating whether the polynomial is a monomial, binomial, or trinomial; then list its terms (entered as a comma-separated list) and state its degree. Polynomial Type Terms Degree -8 Select- Complete the following table by stating whether the polynomial is a monomial, binomial, or trinomial; then list its terms (entered as a comma-separated list) and state its degree. Polynomial Type Terms Degree x-x^2+x^4-x^5- Select-

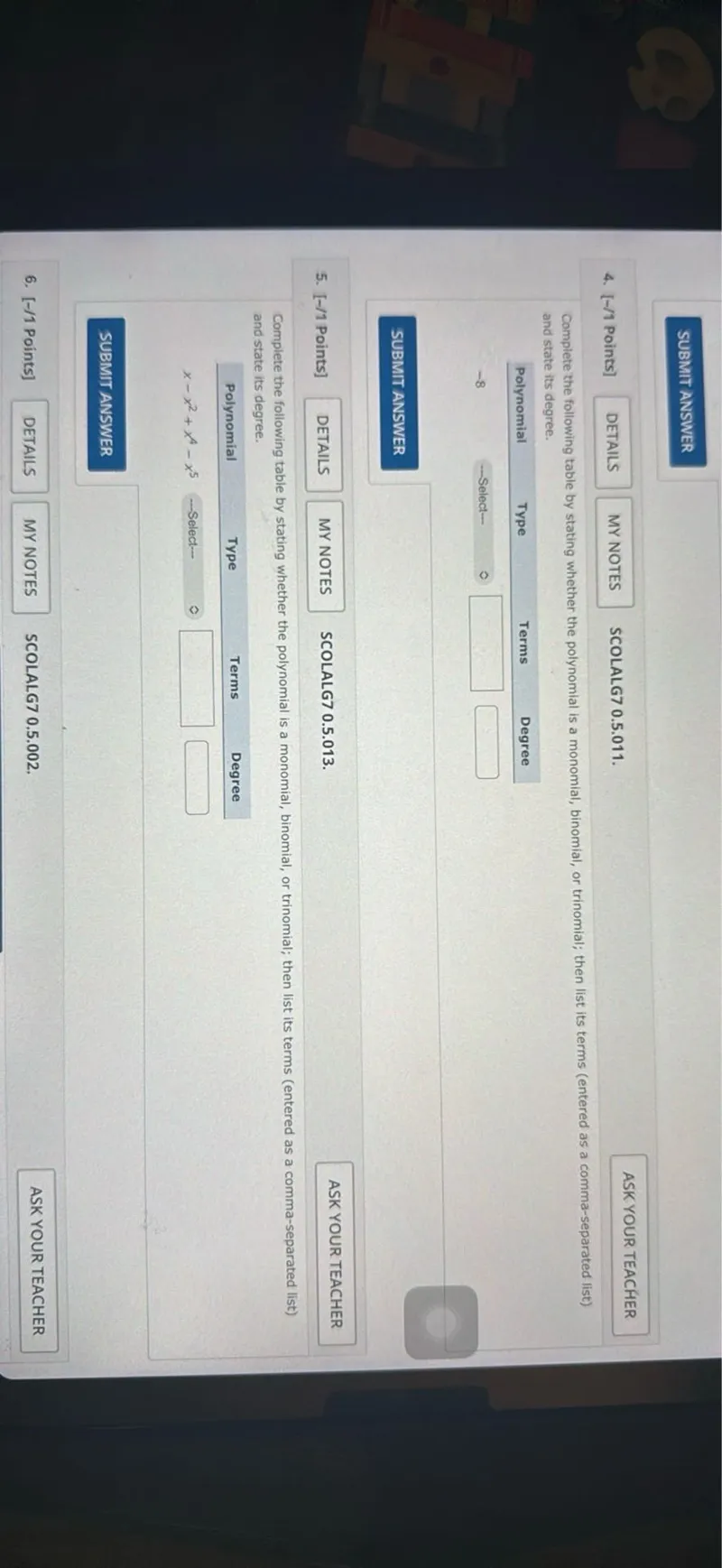
Complete the following table by stating whether the polynomial is a monomial, binomial, or trinomial; then list its terms (entered as a comma-separated list) and state its degree.

Polynomial Type Terms Degree
-8 Select-

Complete the following table by stating whether the polynomial is a monomial, binomial, or trinomial; then list its terms (entered as a comma-separated list) and state its degree.

Polynomial Type Terms Degree
x-x^2+x^4-x^5- Select-

Transcript text: Complete the following table by stating whether the polynomial is a monomial, binomial, or trinomial; then list its terms (entered as a comma-separated list) and state its degree. \begin{tabular}{llll} Polynomial & Type & Terms & Degree \\ \hline-8 & Select- & $\boxed{ }$ \end{tabular} Complete the following table by stating whether the polynomial is a monomial, binomial, or trinomial; then list its terms (entered as a comma-separated list) and state its degree. \begin{tabular}{cccc} Polynomial & Type & Terms & Degree \\ \hline$x-x^{2}+x^{4}-x^{5}-$ Select- & $\square$ & $\square$ \end{tabular}

Solution

Solution Steps

Step 1: Identify the type of the polynomial $-8$

The polynomial $-8$ consists of a single term. Therefore, it is a monomial.

Step 2: List the terms of the polynomial $-8$

The polynomial $-8$ has only one term, which is $-8$.

Step 3: Determine the degree of the polynomial $-8$

The degree of a constant polynomial (like $-8$) is $0$ because there are no variables present.

Step 4: Identify the type of the polynomial $x - x^{2} + x^{4} - x^{5}$

The polynomial $x - x^{2} + x^{4} - x^{5}$ consists of four terms: $x$, $-x^{2}$, $x^{4}$, and $-x^{5}$. Therefore, it is a polynomial with four terms (not a monomial, binomial, or trinomial).

Step 5: List the terms of the polynomial $x - x^{2} + x^{4} - x^{5}$

The terms of the polynomial are $x$, $-x^{2}$, $x^{4}$, and $-x^{5}$.

Step 6: Determine the degree of the polynomial $x - x^{2} + x^{4} - x^{5}$

The degree of a polynomial is the highest power of the variable. Here, the highest power is $5$ (from the term $-x^{5}$). Therefore, the degree is $5$.