Questions: Geometry > Q. 11 Trigonometric ratios: find a side length UZC Find XY. Write your answer as an integer or as a decimal round XY=

Solution Steps

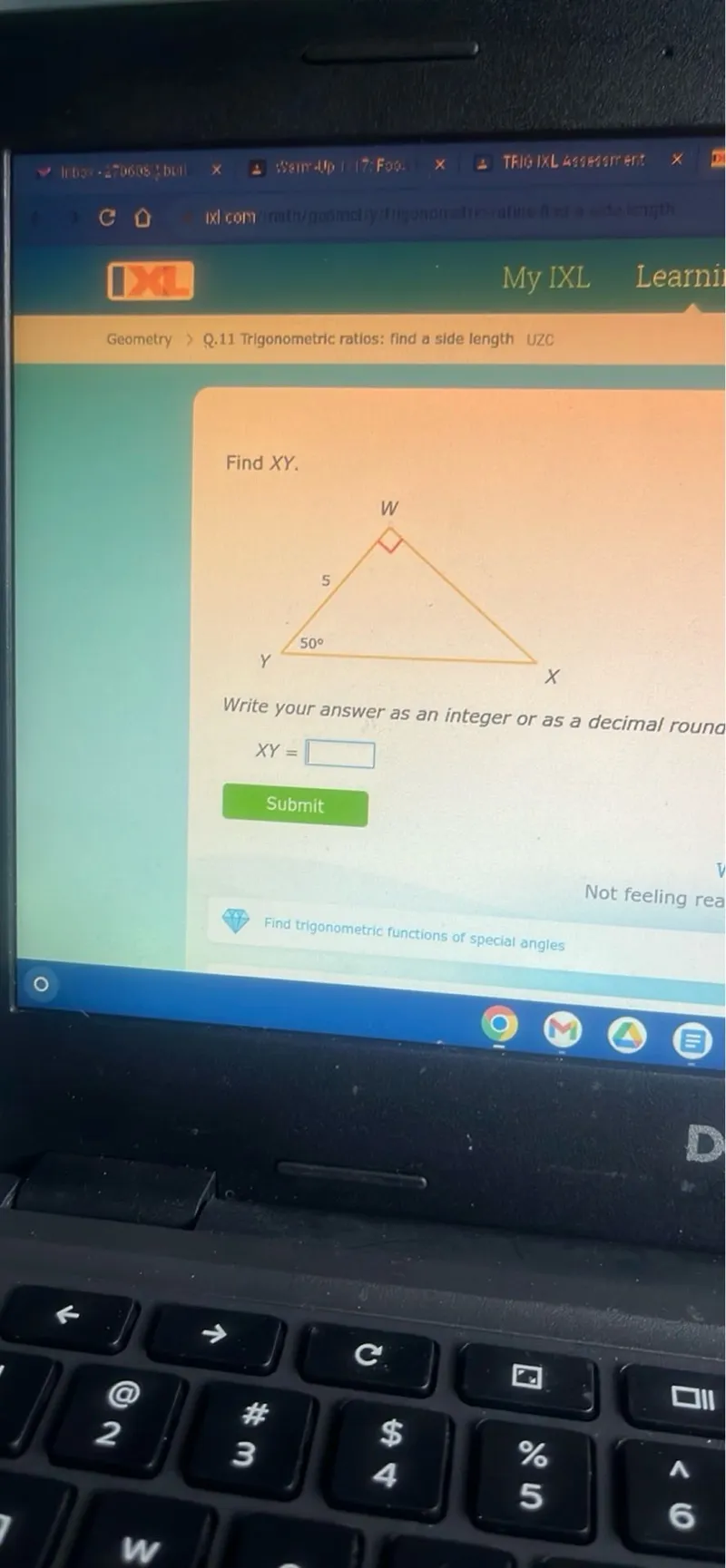
We are given a right triangle $\triangle WXY$ with $\angle W = 90^\circ$, $WY = 5$, and $\angle Y = 50^\circ$. We want to find the length of side $XY$.

We can use the trigonometric ratio involving the adjacent side ($WY$) and the hypotenuse ($XY$) with respect to the given angle $\angle Y$. The cosine function relates these sides and the angle:

$\cos(Y) = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{WY}{XY}$

Substituting the given values, we have:

$\cos(50^\circ) = \frac{5}{XY}$

To solve for $XY$, we can multiply both sides by $XY$ and then divide both sides by $\cos(50^\circ)$:

$XY \cdot \cos(50^\circ) = 5$

$XY = \frac{5}{\cos(50^\circ)}$

Now, we can use a calculator to find the value of $\cos(50^\circ)$ and then calculate $XY$:

$XY \approx \frac{5}{0.6428} \approx 7.7786$

Rounding to the nearest hundredth, we get $XY \approx 7.78$.

Final Answer The final answer is $\boxed{7.78}$