Questions: Choosing the best measure to describe data Answer the questions below. (a) The 10 participants in an experiment had the following reaction times (in milliseconds): 770,772,779,785,796,808,817,818,822,826 Which measure should be used to summarize the data? Mean Median Mode (b) In a survey, a soft drink company asks people to name as many brands of soft drinks as they can. Which measure gives the most frequently mentioned brand? Mean Median Mode (c) In the past 9 days, Jessica has received the following numbers of email advertisements per day: 42,43,46,47,48,49,50,52,86 Which measure should be used to summarize the data? Mean Median Mode

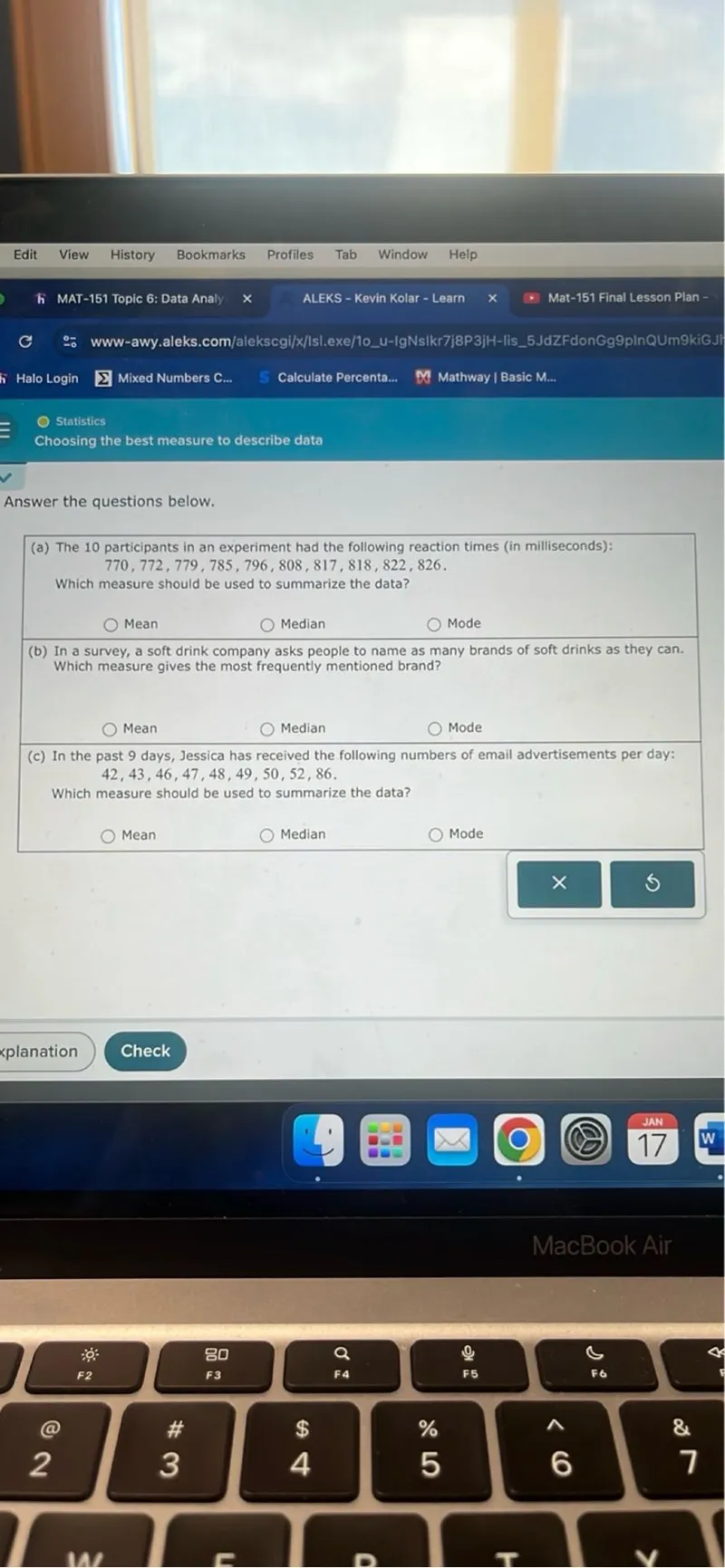
Transcript text: Choosing the best measure to describe data Answer the questions below. (a) The 10 participants in an experiment had the following reaction times (in milliseconds): \[ 770,772,779,785,796,808,817,818,822,826 \] Which measure should be used to summarize the data? Mean Median Mode (b) In a survey, a soft drink company asks people to name as many brands of soft drinks as they can. Which measure gives the most frequently mentioned brand? Mean Median Mode (c) In the past 9 days, Jessica has received the following numbers of email advertisements per day: \[ 42,43,46,47,48,49,50,52,86 \] Which measure should be used to summarize the data? Mean Median Mode

Solution

Solution Steps

Step 1: Determine the appropriate measure for summarizing reaction times

The data provided for reaction times is: \(770, 772, 779, 785, 796, 808, 817, 818, 822, 826\).
Since the data is numerical and there are no extreme outliers, the mean is a suitable measure to summarize the central tendency of the data.

Step 2: Identify the measure for the most frequently mentioned brand

The question asks for the most frequently mentioned brand in a survey.
The mode is the measure that identifies the most frequently occurring value in a dataset, making it the appropriate choice here.

Step 3: Choose the measure for summarizing email advertisements

The data provided for email advertisements is: \(42, 43, 46, 47, 48, 49, 50, 52, 86\).
There is an outlier (\(86\)) in the dataset, which could skew the mean. Therefore, the median is a better measure to summarize the central tendency of the data, as it is less affected by outliers.