Questions: Suppose -x^2+4x-1 ≤ f(x) ≤ x^2-4x+7 for all x values near x=2, except possibly at 2. Evaluate the limit as x approaches 2 of f(x). a.) The limit as x approaches 2 of f(x)=3 b.) The limit as x approaches 2 of f(x) does not exist c.) The limit as x approaches 2 of f(x)=7 d.) The limit as x approaches 2 of f(x)=11
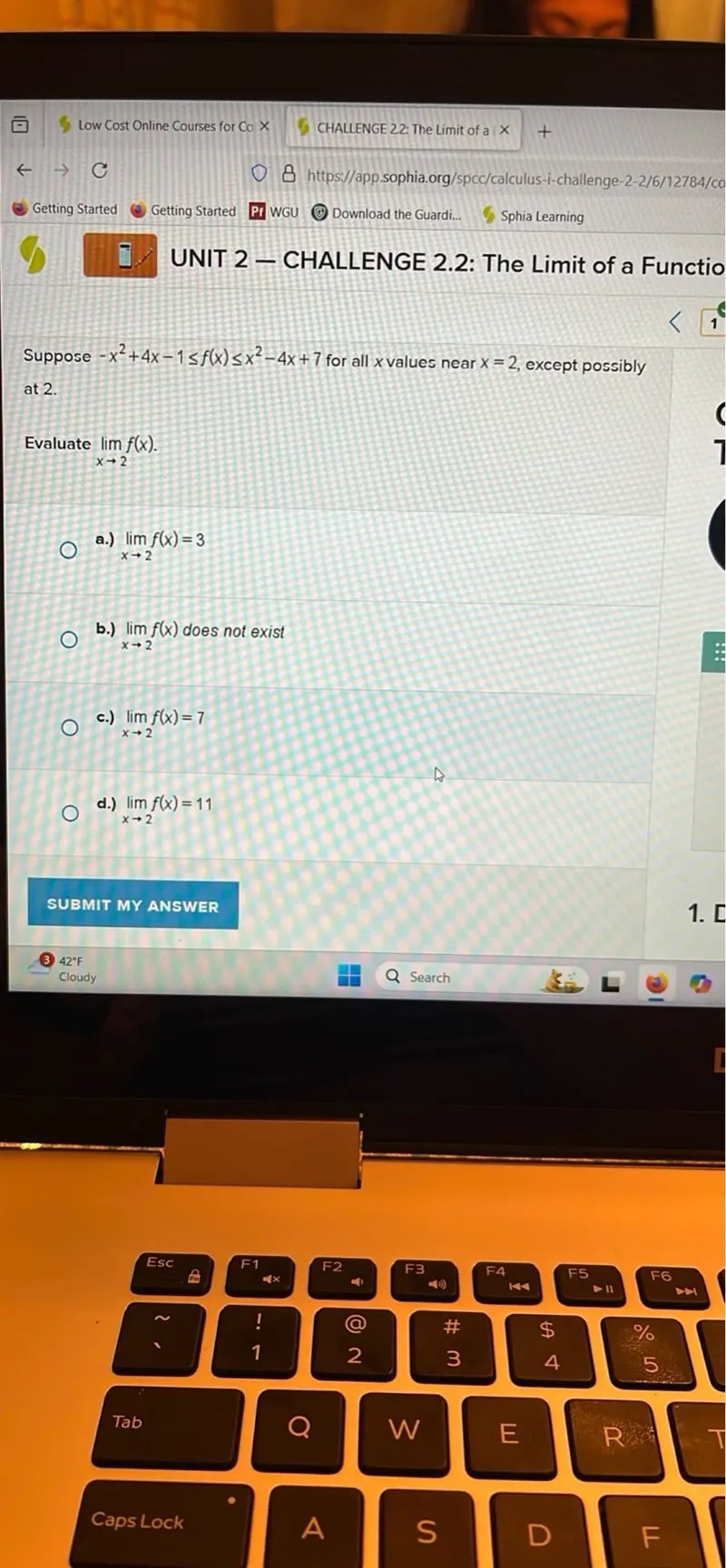
Transcript text: Suppose $-x^{2}+4 x-1 \leq f(x) \leq x^{2}-4 x+7$ for all $x$ values near $x=2$, except possibly at 2 .
Evaluate $\lim _{x \rightarrow 2} f(x)$.
a.) $\lim _{x \rightarrow 2} f(x)=3$
b.) $\lim _{x \rightarrow 2} f(x)$ does not exist
c.) $\lim _{x \rightarrow 2} f(x)=7$
d.) $\lim _{x \rightarrow 2} f(x)=11$





