Questions: What is the measure of angle XYZ? A. 108° B. 75° C. 54° D. 33°
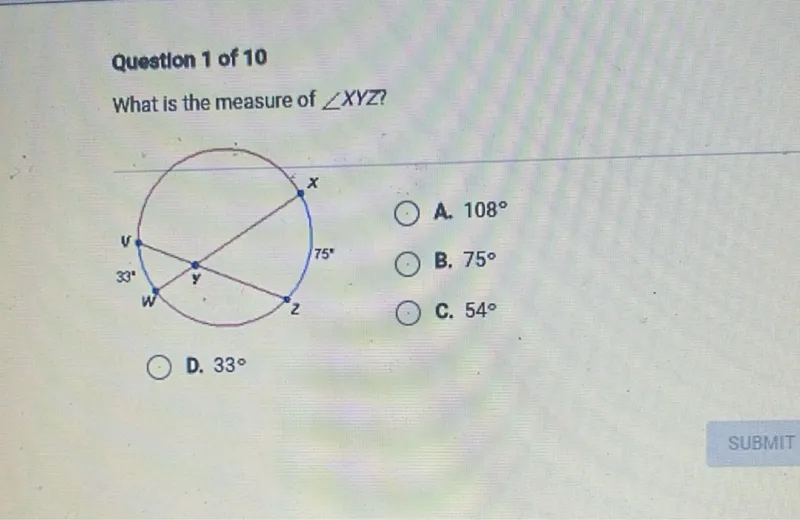
Transcript text: Question 1 of 10
What is the measure of $\angle X Y Z$ ?
A. $108^{\circ}$
B. $75^{\circ}$
C. $54^{\circ}$
D. $33^{\circ}$
SUBMIT





