Questions: Question 2 (6 points) What is the pH of a solution if there are 0.00258 grams of H+ present in 1 L of this solution? Round your answer to one decimal place. Question 3 (6 points) You have two solutions, A and B, separated by a semipermeable membrane. Solution A is 0.5 moles of KCl in 1 LH2O and Solution B is 0.8 moles of dextrose in 1 LH2O. Which side has the higher osmotic pressure at 25°C and what is that pressure? Enter the letter solution with the higher pressure as the Unit. Question 4 (6 points) Over the course of 12 minutes a reaction uses up 120 grams of the reactant Hif. What is the rate of
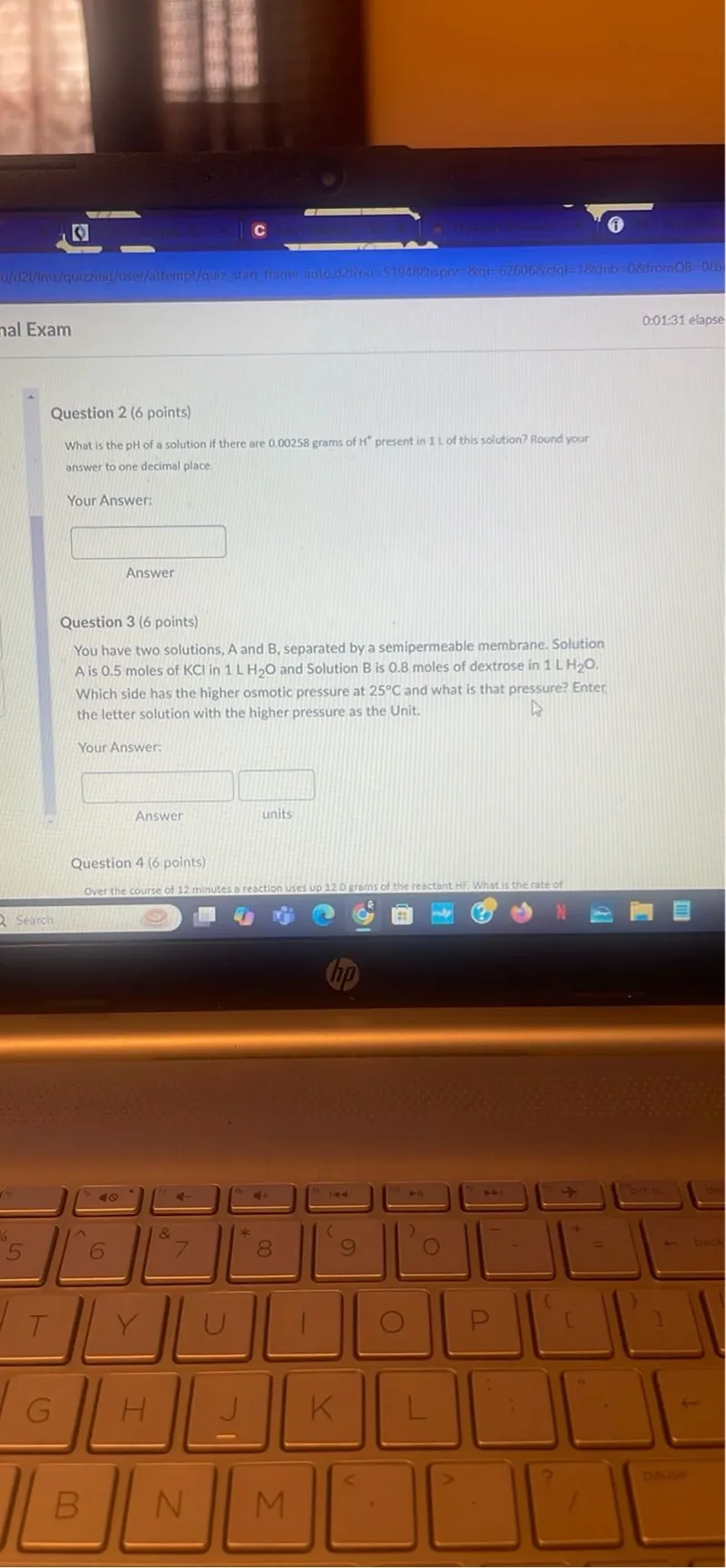
Transcript text: Question 2 ( 6 points)
What is the pH of a solution if there are 0.00258 grams of $\mathrm{H}^{+}$present in 1 L of this solution? Round your answer to one decimal place.
Question 3 ( 6 points)
You have two solutions, $A$ and $B$, separated by a semipermeable membrane. Solution $A$ is 0.5 moles of KCl in $1 \mathrm{LH} \mathrm{H}_{2} \mathrm{O}$ and Solution B is 0.8 moles of dextrose in $1 \mathrm{LH} \mathrm{H}_{2} \mathrm{O}$. Which side has the higher osmotic pressure at $25^{\circ} \mathrm{C}$ and what is that pressure? Enter the letter solution with the higher pressure as the Unit.
Question 4 ( 6 points)
Over the course of 12 minutes a reaction uses up 120 grams of the reactant Hif, What is the rate of





