Questions: Find the exact values of the six trigonometric functions of the given angle. Do not use a calculator. pi/3 Select the correct choice below and fill in any answer boxes within your choice. sin(pi/3) = sqrt(3)/2 (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined. Select the correct choice below and fill in any answer boxes within your choice. A. cos(pi/3) = 1/2 (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined. Select the correct choice below and fill in any answer boxes within your choice. A. tan(pi/3) = sqrt(3) (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined.

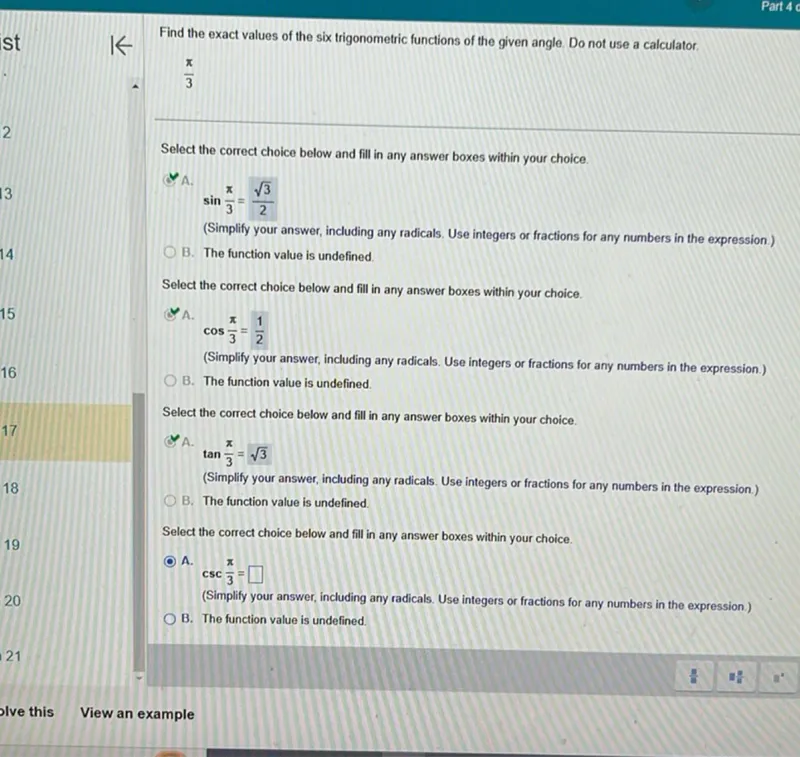
$Find the exact values of the six trigonometric functions of the given angle. Do not use a calculator. pi/3 Select the correct choice below and fill in any answer boxes within your choice. sin(pi/3) = sqrt(3)/2 (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined. Select the correct choice below and fill in any answer boxes within your choice. A. cos(pi/3) = 1/2 (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined. Select the correct choice below and fill in any answer boxes within your choice. A. tan(pi/3) = sqrt(3) (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined.$

Transcript text: Find the exact values of the six trigonometric functions of the given angle. Do not use a calculator. \[ \frac{\pi}{3} \] Select the correct choice below and fill in any answer boxes within your choice. $\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$ (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined. Select the correct choice below and fill in any answer boxes within your choice. A. $\cos \frac{\pi}{3}=\frac{1}{2}$ (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined. Select the correct choice below and fill in any answer boxes within your choice. A. $\tan \frac{\pi}{3}=\sqrt{3}$ (Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) B. The function value is undefined.

Solution

Solution Steps

Step 1: Find $\sin \frac{\pi}{3}$

The sine of $\frac{\pi}{3}$ is a well-known value from the unit circle. It corresponds to $\frac{\sqrt{3}}{2}$. Therefore, the correct choice is: \[ \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2} \]

Step 2: Find $\cos \frac{\pi}{3}$

The cosine of $\frac{\pi}{3}$ is also a standard value from the unit circle. It corresponds to $\frac{1}{2}$. Therefore, the correct choice is: \[ \cos \frac{\pi}{3} = \frac{1}{2} \]

Step 3: Find $\tan \frac{\pi}{3}$

The tangent of $\frac{\pi}{3}$ is calculated as the ratio of sine to cosine: \[ \tan \frac{\pi}{3} = \frac{\sin \frac{\pi}{3}}{\cos \frac{\pi}{3}} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} \] Therefore, the correct choice is: \[ \tan \frac{\pi}{3} = \sqrt{3} \]

Final Answer

$\sin \frac{\pi}{3} = \frac{\sqrt{3}}{2}$, $\cos \frac{\pi}{3} = \frac{1}{2}$, $\tan \frac{\pi}{3} = \sqrt{3}$, $\csc \frac{\pi}{3} = \frac{2}{\sqrt{3}}$ (or $\frac{2\sqrt{3}}{3}$ after rationalizing).

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!