Questions: Video Part 1: Graph The position vs. time graph below is for an object that is exhibiting SHM. The position function is: x(t)=A cos(ωt+Φ). Use this graph to fill in the table. A (m) T (s) f (Hz) vmax (m / s) 1 Part 2: Block on a horizontal surface Part 3: Finding v Part 4: Finding x
Transcript text: Video
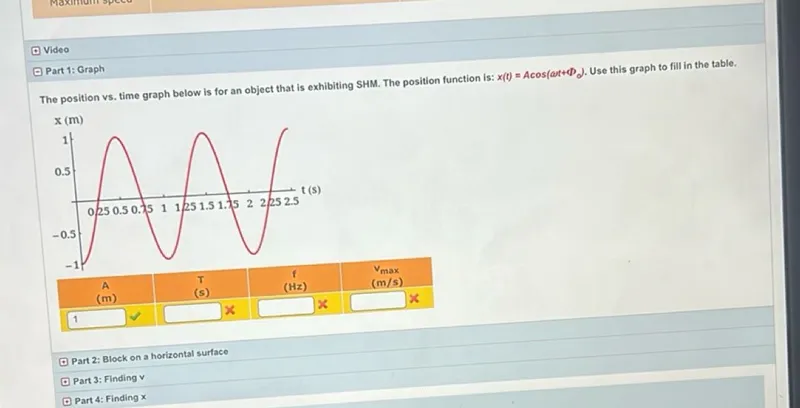
Part 1: Graph
The position vs. time graph below is for an object that is exhibiting SHM. The position function is: $x(t)=A \cos (\omega t+\Phi)$. Use this graph to fill in the table.
\begin{tabular}{|c|c|c|c|}
\hline \begin{tabular}{c}
A \\
$(\mathrm{m})$
\end{tabular} & \begin{tabular}{c}
T \\
$(\mathrm{s})$
\end{tabular} & \begin{tabular}{c}
$\mathbf{f}$ \\
$(\mathrm{Hz})$
\end{tabular} & \begin{tabular}{c}
$\mathbf{v}_{\text {max }}$ \\
$(\mathrm{m} / \mathrm{s})$
\end{tabular} \\
\hline 1 & & \\
\hline
\end{tabular}
Part 2: Block on a horizontal surface
Part 3: Finding $v$
Part 4: Finding $x$





