Questions: Simplify the following expression. Express your answer using the same notation as the original expression. x^(4/3) y^(1/2) / x^(-5/3) y

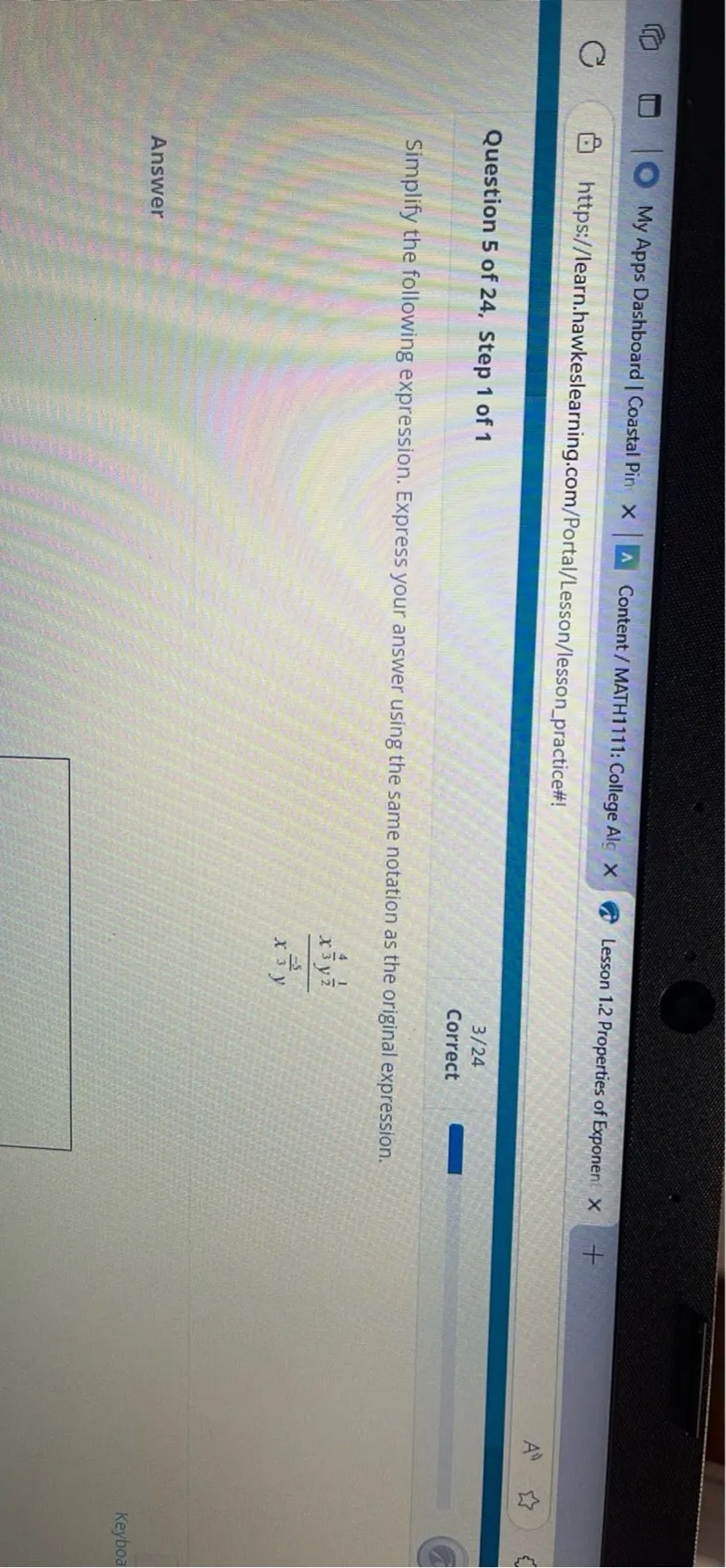
Simplify the following expression. Express your answer using the same notation as the original expression. x^(4/3) y^(1/2) / x^(-5/3) y
Transcript text: Simplify the following expression. Express your answer using the same notation as the original expression. \[ \frac{x^{\frac{4}{3}} y^{\frac{1}{2}}}{x^{\frac{-5}{3}} y} \]
failed

Solution

failed
failed

Solution Steps

Step 1: Simplify the exponents of \( x \)

\[ \frac{x^{\frac{4}{3}}}{x^{\frac{-5}{3}}} = x^{\frac{4}{3} - \left(-\frac{5}{3}\right)} = x^{\frac{4}{3} + \frac{5}{3}} = x^{\frac{9}{3}} = x^3 \]

Step 2: Simplify the exponents of \( y \)

\[ \frac{y^{\frac{1}{2}}}{y} = y^{\frac{1}{2} - 1} = y^{-\frac{1}{2}} \]

Step 3: Combine the simplified terms

\[ x^3 \cdot y^{-\frac{1}{2}} = \frac{x^3}{y^{\frac{1}{2}}} \]

Final Answer

\(\boxed{\frac{x^3}{y^{\frac{1}{2}}}}\)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Analyzing Distance and Time The turtle's distance from his starting point is increasing between seconds. The turtle's distance from his starting point is constant between seconds. The turtle's distance from his starting point is decreasing between seconds.
failedAnswered
Find the intervals on which f(x) is increasing, the intervals on which f(x) is decreasing, and the local extrema, f(x)=x^3+5x-14 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The function is increasing on . (Type your answer using interval notation. Type integers or simplified fractions. Use a comma to separate answers as needed.) B. The function is never increasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The function is decreasing on . (Type your answer using interval notation. Type integers or simplified fractions. Use a comma to separate answers as needed.) B. The function is never decreasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (Type integers or simplified fractions. Use a comma to separate answers as needed.) A. The function has local maxima f(c)= and local minima f(c)= . B. The function has local minima f(c)= , and no local maxima.
failedAnswered
toras AMt Thu dan 2 assignments.pennfoster.com Ieseon a Ixam Exam Lesson Name: States of Matter, Stoichiometry, and Phase Changes Exam number: 700634RR Exam Guidelines Exam Instructions Question 15 of 20 : Select the best answer for the question. 15. A gas in a 6.2 mL cylinder has a pressure of 1.4 atmospheres. A piston is pushed in until the gas volume is 3.1 mL , while the temperature remains constant. What's the final pressure of the gas in the cylinder? A. 5.6 atm B. 2.8 atm C. 4.8 atm D. 3.2 atm Mark for review (Will be highlighted on the review page) <<Previous Question Next Question >> Review My Answers Save
failedAnswered
For 39 nations, a correlation of 0.863 was found between y= Internet use (%) and x= gross domestic product (GDP, in thousands of dollars per capita). The regression equation is y^=-3.37+1.53 x. Complete parts (a) through (c). a. Based on the correlation value, the slope had to be positive. Why? A. That is a very unusual fact, because the slope and correlation usually have different signs. B. Although slope and correlation usually have different values, they always have the same sign. C. The slope and correlation are positive because gross domestic product could not be negative. D. The correlation and the slope are positive because the y-intercept is negative. b. One nation had a GDP of 25.6 thousand dollars and Internet use of 30.6 %. Find its predicted Internet use based on the regression equation. % (Round to one decimal place as needed.) c. Find the residual for this nation. (Round to one decimal place as needed.)
failedAnswered
Suppose that the cost, p, of shipping a 3-pound parcel depends on the distance shipped, x, according to the function p(x) depicted in the graph. Find each limit, if it exists. lim x → 500− p(x), lim x → 500 p(x), lim x → 500+ p(x) A. 5 ; 10,10 B. 5 , does not exist; 10 C. 5 ; 5 ; 10 D. 5 ; does not exist, does not exist