Questions: Given the function f(x)=∫(from 1 to x)(t^3+15t^2+54t) dt determine all intervals on which f is decreasing.

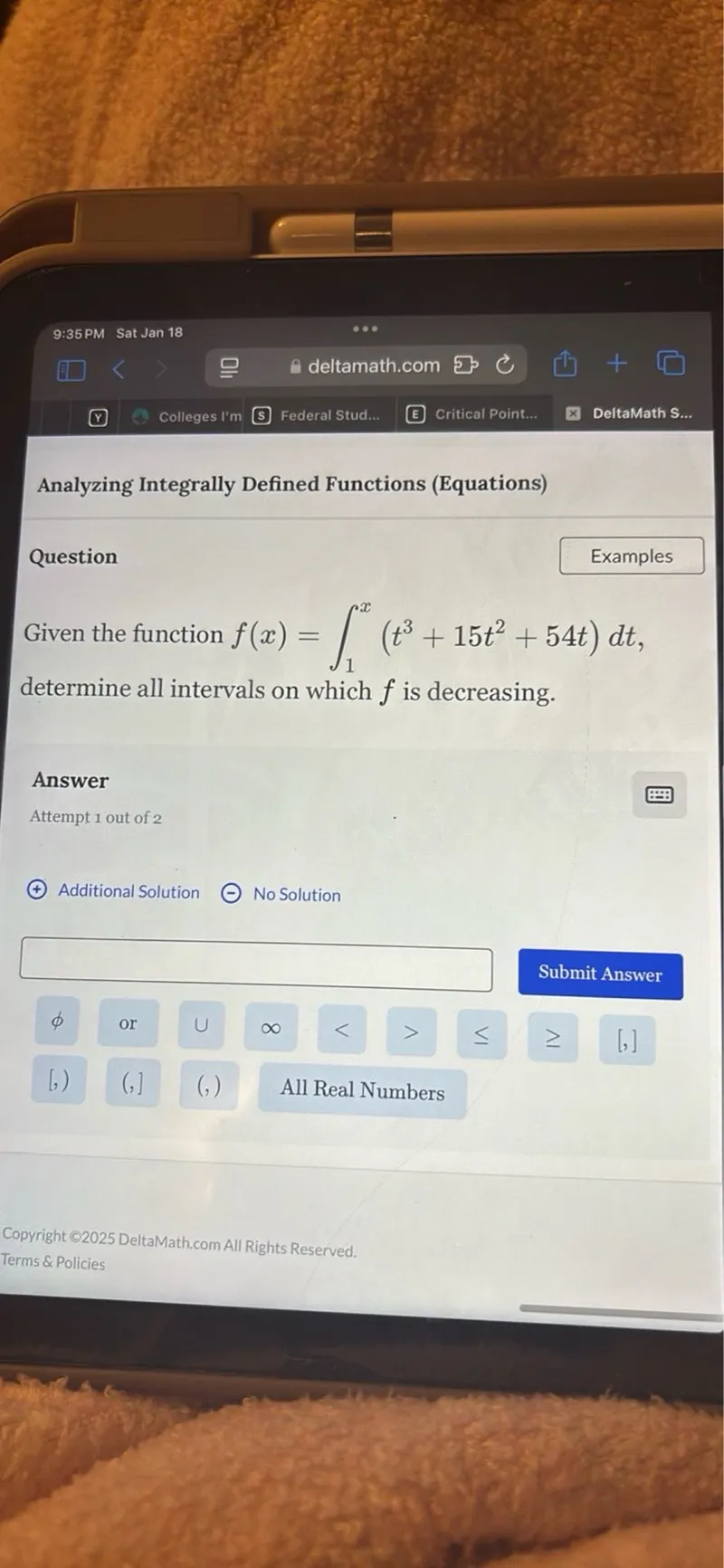
Transcript text: Given the function $f(x)=\int_{1}^{x}\left(t^{3}+15 t^{2}+54 t\right) d t$ determine all intervals on which $f$ is decreasing.

Solution

Solution Steps

Step 1: Find the Derivative

To determine where the function $ f(x) $ is decreasing, we first compute its derivative: \[ f'(x) = x^3 + 15x^2 + 54x \]

Step 2: Set Up the Inequality

Next, we set up the inequality to find where the derivative is negative: \[ f'(x) < 0 \]

Step 3: Solve the Inequality

We solve the inequality $ x^3 + 15x^2 + 54x < 0 $. The critical points where the derivative equals zero are found, and we analyze the sign of $ f'(x) $ in the intervals determined by these points. The solution reveals that $ f(x) $ is decreasing in the intervals: \[ (-\infty, -9) \quad \text{and} \quad (-6, 0) \]

Final Answer

The function $ f(x) $ is decreasing on the intervals $ (-\infty, -9) $ and $ (-6, 0) $. Thus, the final answer is: \[ \boxed{(-\infty, -9) \cup (-6, 0)} \]

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!