Questions: Derive the reduced modulus of elasticity Er for an idealized I-section shown in Fig. P2.12, in which it is assumed that one-half of the cross-section area is concentrated in each flange and the area of the web is disregarded.

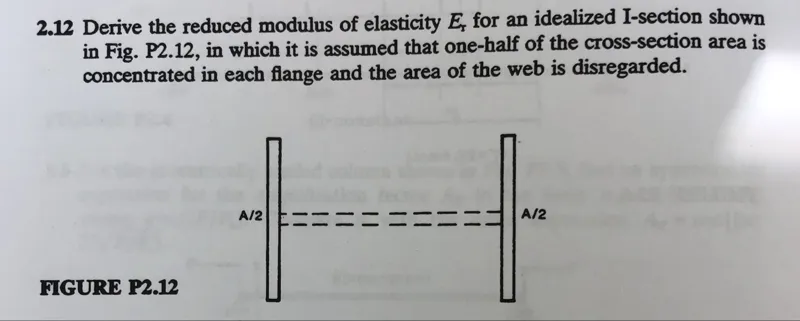
Derive the reduced modulus of elasticity \(E_r\) for the given I-section. Define the given parameters. The cross-sectional area is divided equally between the two flanges: \(A_f = A/2\) for each flange. The web area is neglected. Express the bending stress in each flange. Let \(M\) be the bending moment, \(y\) be the distance from the neutral axis to the centroid of each flange, and \(I\) be the moment of inertia of the section. The bending stress \(\sigma\) in each flange is given by \(\sigma = My/I\). Since the flanges are equidistant from the neutral axis, \(y\) is the same for both. Calculate the moment of inertia \(I\). Since the web is neglected, the moment of inertia \(I\) is given by \(I = 2A_f y^2 = 2(A/2)y^2 = Ay^2\). Express the strain in each flange. The strain \(\epsilon\) in each flange is given by \(\epsilon = \sigma/E\), where \(E\) is the modulus of elasticity. Substituting the expression for \(\sigma\), we get \(\epsilon = My/(EI)\). Relate the bending moment to the curvature. The curvature \(\kappa\) is given by \(\kappa = 1/R\), where \(R\) is the radius of curvature. The relationship between bending moment and curvature is \(M = EI\kappa = EI/R\). Substituting this into the expression for strain, we get \(\epsilon = (EI/R)y/(EI) = y/R = y\kappa\). Express the axial stress and strain. The axial stress \(\sigma_a\) is given by \(\sigma_a = P/A\), where \(P\) is the axial load and \(A\) is the total cross-sectional area. The axial strain \(\epsilon_a\) is given by \(\epsilon_a = \sigma_a/E = P/(AE)\). Relate the bending stress to the reduced modulus. The reduced modulus \(E_r\) is defined as the ratio of bending stress to strain when both axial load and bending moment are present. We can express this as \(\sigma = E_r \epsilon\). In this case, \(\sigma = My/I\) and \(\epsilon = y\kappa\). Therefore, \(E_r = M/(I\kappa) = EI/I = E\).

\(\boxed{E_r = E}\)

\(\boxed{E_r = E}\)