Questions: Use the graph of y=q(x) to determine the following limits. Use DNE for "does not exist" when applicable. a. lim x → 7 q(x)= -1 b. lim x → 7+ q(x)=0 c. lim x → 7 q(x)=DNE

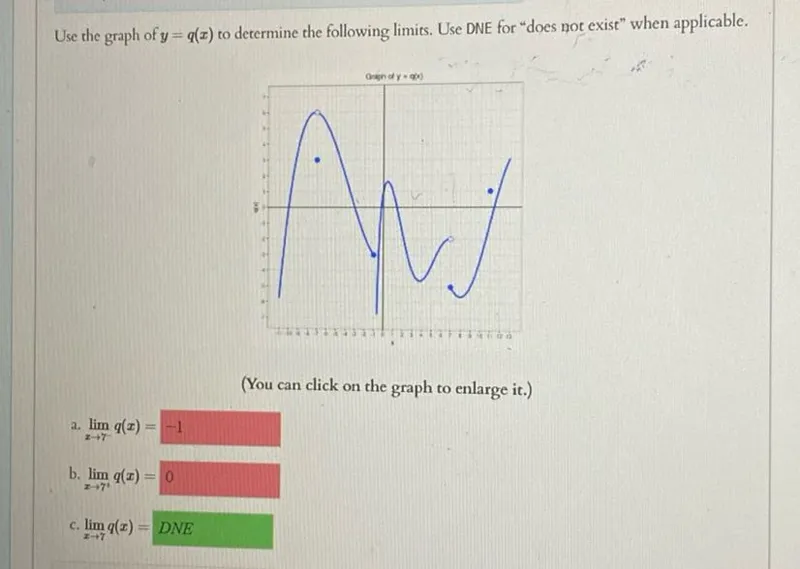
Transcript text: Use the graph of $y=q(x)$ to determine the following limits. Use DNE for "does not exist" when applicable. a. $\lim _{x \rightarrow 7} q(x)=$ $\square$ $-1$ b. $\lim _{x \rightarrow 7^{+}} q(x)=0$ $\square$ c. $\lim _{x \rightarrow 7} q(x)=D N E$

Solution

Solution Steps

Step 1: Analyze the limit as x approaches 7 from the left.

We observe the graph of $y = q(x)$ as $x$ approaches 7 from the left ($x \rightarrow 7^{-}$). The value of $q(x)$ approaches -1. So, $\lim_{x \rightarrow 7^{-}} q(x) = -1$.

Step 2: Analyze the limit as x approaches 7 from the right.

We observe the graph of $y = q(x)$ as $x$ approaches 7 from the right ($x \rightarrow 7^{+}$). The value of $q(x)$ approaches -1. So, $\lim_{x \rightarrow 7^{+}} q(x) = -1$.

Step 3: Analyze the limit as x approaches 7.

Since $\lim_{x \rightarrow 7^{-}} q(x) = -1$ and $\lim_{x \rightarrow 7^{+}} q(x) = -1$, the limit as $x$ approaches 7 is -1. So, $\lim_{x \rightarrow 7} q(x) = -1$.

Final Answer

a. $\boxed{-1}$ b. $\boxed{-1}$ c. $\boxed{-1}$

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

Next >

Thank you for your feedback.

Copied!