Questions: Sketch the graph of the polynomial function. f(x)=2x^4+3x^3-8x^2+3x Choose the correct graph below. A. B. C. D.

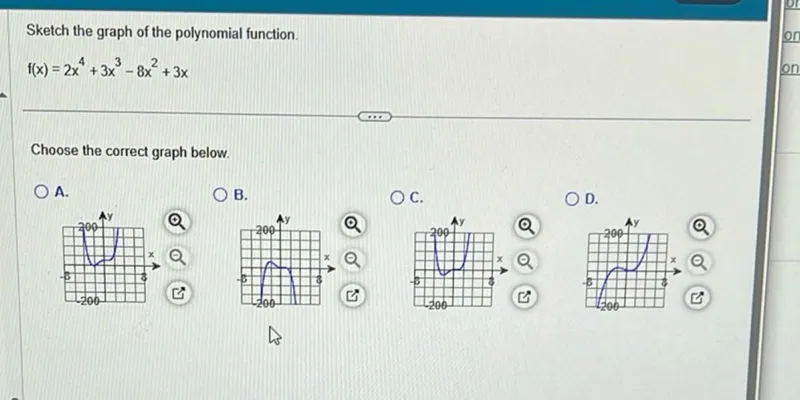
Sketch the graph of the polynomial function f(x) = 2x⁴ + 3x³ - 8x² + 3x. Determine the end behavior. The leading term is 2x⁴. Since the degree is even and the leading coefficient is positive, the graph rises to the left and rises to the right. Find the y-intercept. f(0) = 2(0)⁴ + 3(0)³ - 8(0)² + 3(0) = 0. So the y-intercept is (0,0). Find the x-intercepts. Factor the function: f(x) = x(2x³ + 3x² - 8x + 3). Factoring the cubic is difficult by hand. However, we can use a graphing calculator or software to find the approximate roots of 2x³ + 3x² - 8x + 3 = 0, which are approximately x ≈ -2.6, x ≈ 0.5 and x ≈ 1.1. Analyze the graph behavior near the intercepts. Since each root has multiplicity one, the graph passes through the x-axis at each intercept. Use a graphing tool to plot the function. Using a graphing tool, we can observe that the correct graph matches the described end behavior and x-intercepts. \( \boxed{\text{C}} \)

\( \boxed{\text{C}} \)